1. Estimators
1.1 Parameters and Estimators
Recall that
- Parameter: unknown object of interest
- Estimator: data-driven guess of the value of the
parameter
- e.g. Binomial distribution has one unknown parameter: the probability of success, \(\pi\).
- The other parameter, \(n\), is usually dictated by the researcher in terms of the size of a sample that will be obtained.
2. Review Binomial Random Variable
- There are four conditions that characterize
binomial data.
- 1> The outcome or response takes on one and only one of two
possibilities. This is a binary outcome or
binary response.
- The outcome of interest = success
- The other = failure
- Success does not necessarily mean that it is a ‘desirable’ outcome. For example, we may be interested in whether a patient dies or lives in hospital. In this case, we might denote the outcome death as a ‘success’ if it were the outcome of interest.
- 2> The outcome is observed a known number of times. One
observation of the outcome is sometimes called a Bernoulli
trial. A binomial random variable is an observation of a set
number, \(n\) of
Bernoulli trials.
- A trial can be something like an individual attempt or try such as a flip of a coin.
- The outcome of interest = heads (maybe)
- A trial could also be an individual and an outcome of interest is whether the individual tests positive for a disease.
- 3> The chance, or probability, that a particular outcome occurs
is the same for each trial.
- If we are sampling individuals, they all come from the same population and have the same chance of being created.
- If it is a test result, it assumes that the testing procedure is the same for each sample.
- 4> The outcome of one trial must not be influenced by the
outcomes of other trials. (Independency)
- An example where this is not met if when testing for disease, there was contamination between the samples.
- 1> The outcome or response takes on one and only one of two
possibilities. This is a binary outcome or
binary response.
- Binomial distribution depends on two parameters.
- \(n\): the number of trials (or number of individuals)
- \(\pi\): the
probability of a sucess in ONE trial
- If \(\pi\), the probability of success, is close to 1, then the number of successes out of \(n\) trials will tend to be large, or closer to \(n\).
- If \(\pi\), the probability of success, is near 0, \(Y\) will tend to be closer to 0.
- Binomial random variable, \(Y\): the count of the number of
successes in \(n\) trials
- the values that Y can be are 0, 1, 2, …, n.
3. Estimate the value of \(\pi\) for a binomial random variable.
- The mean of binomial random variable \(Y\) with parameters \(n\) and \(\pi\) is \(E(Y)=n\pi\).
- To estimate the proportion of success for a
binomial random variable, we can use the sample
proportion of the observed sample.
- To estimate \(\pi\), we would divide the observed number of successes, \(y\), by \(n\).
\[ E\left(\frac{Y}{n}\right)=\pi \]
- So the estimate of \(\pi\), which we will call \(p\), is
\[ p=\frac{y}{n} \]
where \(y\) is the observed number of successes in the \(n\) trials.
3.1 Example: estimate the proportion of individuals who have diabetes
It is known that the proportion of adults in the US who have diabetes is 0.094 or 9.4%. If we take a random sample of 750 of US adults and determine the number who have diabetes, \(Y\), then \(Y\) has a binomial distribution with \(n\)=750 and \(\pi\)=0.094. Suppose we did not know the value of \(\pi\), we would estimate it with the observed number of individuals out of the 750 who have diabetes, \(y\) divided by 750; the estimate would be \(p\) = \(y\) / 750.
1> Let’s simulate this experiment by using the R
function rbinom() to get a sample size 750
from the population
(y <- rbinom(1, 750, 0.094))## [1] 682> Based on the sample above, the estimate of \(\pi\) would be \(p\) = 80 / 750 = 0.107. What happens if we take another sample from the population of size 750?
(y1 <- rbinom(1, 750, 0.094))## [1] 73- Based on this another sample, the estimate of \(\pi\) would be \(p\)=72/750=0.096.
- The two estimates are not equal to each other.
- It means the estimate \(p\) varies from sample to sample
- Can we characterize this variability? (Yes, by simulation)
Perform a simulation where we get 5000 samples of size 750 each and for each sample, we compute the value of \(p\).
- Use
rbinom()and store the 5000 simulated estimates of \(p\) in a vector calledprops. We then will take a look at the first 125 values in the vector.
props <- rbinom(5000, 750, 0.094) / 750
round(props[1:125], 3)## [1] 0.108 0.116 0.079 0.092 0.068 0.093 0.079 0.084 0.085 0.077 0.093 0.088
## [13] 0.089 0.097 0.064 0.099 0.093 0.084 0.093 0.085 0.093 0.065 0.100 0.081
## [25] 0.081 0.065 0.103 0.117 0.101 0.087 0.072 0.097 0.100 0.099 0.089 0.076
## [37] 0.097 0.097 0.084 0.107 0.087 0.099 0.117 0.089 0.081 0.104 0.091 0.091
## [49] 0.083 0.096 0.096 0.097 0.111 0.100 0.105 0.091 0.107 0.093 0.105 0.104
## [61] 0.100 0.105 0.108 0.091 0.091 0.091 0.083 0.119 0.120 0.101 0.101 0.101
## [73] 0.103 0.088 0.093 0.089 0.088 0.100 0.093 0.115 0.097 0.085 0.091 0.091
## [85] 0.084 0.081 0.104 0.089 0.100 0.107 0.079 0.100 0.095 0.099 0.089 0.112
## [97] 0.113 0.100 0.096 0.104 0.097 0.084 0.092 0.095 0.089 0.095 0.085 0.083
## [109] 0.093 0.101 0.091 0.104 0.079 0.105 0.085 0.097 0.108 0.079 0.083 0.113
## [121] 0.087 0.085 0.085 0.096 0.101- Looking at the values, they all seem relatively close to the real value of 0.094.
- Looking at the data through the graph is better.
hist(props,
xlab = "sample proportion with diabetes",
ylab = "probability",
freq = FALSE,
main = "Estimated Sampling Distribution")
lines(density(props,adjust=2.5),col="red",lwd=4)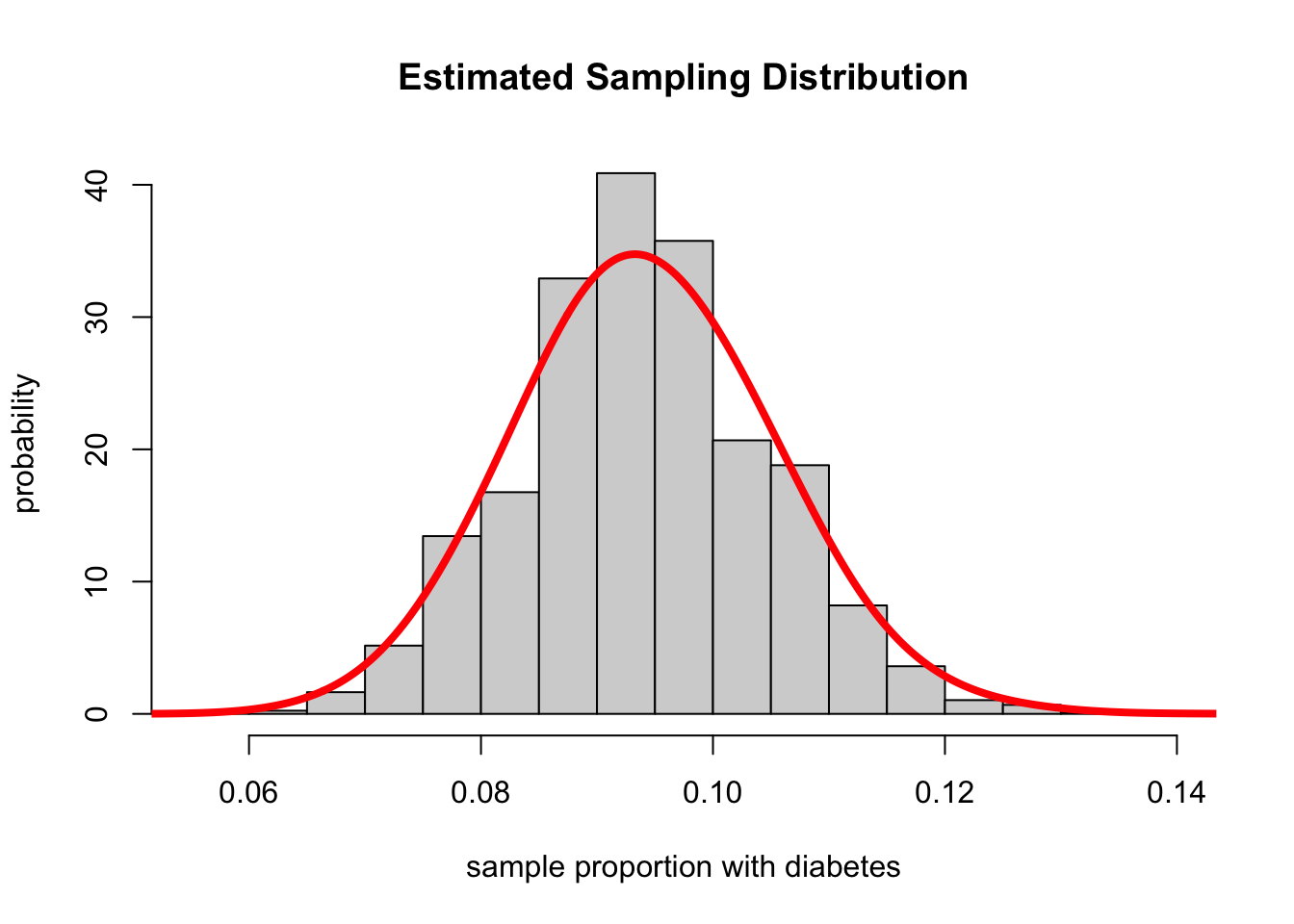
- The plot shows both the histogram and the density plot.
- We could use this information in our simulated sampling distribution to determine the likelihood of getting various estimates for the proportion of individuals with diabetes based on a random sample of size 750.
What is the probability of getting an estimate for the proportion with diabetes between 0.084 and 0.104, inclusive?
sum((props >= 0.084 & props <= 0.104)) / 5000## [1] 0.6844It would be quite likely to get estimates in this range. This can also be seen from the sampling distribution for the estimated proportion.
What is the probability of getting an estimate for the proportion with diabetes that is more than 0.02 from the true value?
the interval is (0.094-0.02, 0.094+0.02) = (0.074, 0.114)
(answer <- sum((props < 0.074 | props > 0.114 )) / 5000)## [1] 0.061Hence we can see that with a sample of 750, we are unlikely to get a estimate that is more than 0.061 from the real proportion.
3.2 Estimators as random variables
- a function of random variables is a random variable.
- Thus, estimators are random variables.
- As such, we can compute the expected value and the variance of the estimator.
3.3 Mean and Variance of estimate the proportion of success for a binomial random variable
1) mean
The estimator of the probability of success for the binomial distribution is itself a random variable.
The number of observed successes in the sample, \(y\), is described by the random variable \(Y\), which is binomial.
So our estimator is the random variable, Y/n, we can compute its expected value.
\[ E(p)=E\left(\frac{Y}{n}\right)=\frac{E(Y)}{n}=\frac{n \pi}{n}=\pi \]
So the expected value of the estimator is in this case equal to the true parameter value.
- The estimators that have this property are called unbiased.
The expected value of this estimator does NOT depend on the sample size \(n\) upon which the estimate is based.
- It means that on average, the estimate will equal the value we are trying to estimate.
2) variance
- The variance of the estimator decreases as the sample size
increases.
- In order to ensure that the estimate of the true proportion is closer to the true proportion, one needs a larger sample size.
We want estimators that have the mean as close as possible to the true value and smallest variance.
4. Sampling distribution for the estimate of a binomial proportion
- A basic statistical fact is that sample statistics (e.g. the sample proportion, \(p = y / n\) , where y is the number of successes in a sample of size n) vary from sample to sample.
- The key idea is that a statistic associated with a random sample is a random variable.
- We can relate the variability of a statistic based on a random sample to the variability of the random variable on which the statistic is based.
The probability function (PMF or PDF) of a statistic is called the
sampling distribution of the statistic.
4.1 Characteristics of the Sample Proportion
If a random variable \(Y\) is binomial
- with a probability of success of \(\pi\),
- the sampling distribution of the sample proportion (of samples of size \(n\)) :
has population mean \(\pi\) and population variance \(\frac{\pi(1-\pi)}{n}\).
Standard error: the standard deviation of the sampling distribution.
Looking at the sampling distribution of the sample proportion, \(p\), its shape is similar to a binomial distribution.
If the binomial distribution of \(Y\) with parameters \(\pi\) and \(n\) can only take the values of \(y\) = 0, 1, 2, . . . , \(n\), then the distribution of the sample proportion can only take on the values \(p\) = 0/\(n\)(= 0), 1/\(n\), 2/\(n\), . . . , \(n\)/\(n\)(= 1).
The probabilities map one-to-one with the probability
\[ \begin{array}{c}\operatorname{Pr}(Y=0)=\operatorname{Pr}(p=0) \\ \operatorname{Pr}(Y=1)=\operatorname{Pr}(p=1 / n) \\ \operatorname{Pr}(Y=2)=\operatorname{Pr}(p=2 / n) \\ \operatorname{Pr}(Y=3)=\operatorname{Pr}(p=3 / n) \\ \ldots \\ \operatorname{Pr}(Y=n)=\operatorname{Pr}(p=1)\end{array} \]
- So the sampling distribution for the sample proportion \(p\)=\(y\) / \(n\) has binomial probabilities but with different outcome values.
If \(Y\) has a binomial distribution with a probability of success of \(\pi\), then the sample proportion \(p\), based on a random sample of \(n\) observations (or trials), has a binomial distribution with men \(\pi\) and variance \(\pi(1-\pi)\) /\(n\).
In order to compute these values, we need to usebinom()with \(Y\) and \(n\) to get the probabilities.
What is the probability of getting an estimate for the proportion with diabetes between 0.084 and 0.104, inclusive?
First, we need to determine the \(y\) values that corresponds to 0.084 and 0.104, respectively. \(\operatorname{Pr}(63 \leq Y \leq 78)\)
(answer2 <- round(pbinom(78, 750, 0.094) - pbinom(62, 750, 0.094), 3))## [1] 0.683Second, compare 0.683 to the below:
sum((props >= 0.084 & props <= 0.104)) / 5000## [1] 0.6844What is the probability of getting an estimate for the proportion with diabetes that is more than 0.02 from the true value?
- The interval is (0.094-0.02, 0.094+0.02) = (0.074, 0.114)
- Pr(\(p\)<0.074) + Pr(\(p\)>0.114) To translate to the values for Y, we multiply the \(p\) by 750. This results in \(y=750\times0.074=55.5\) and \(y=750\times0.114=85.5\). Thus, we want to use a binomial distribution to compute \(Pr(Y<55.5)=Pr(Y\le 55)\) and compute \(Pr(Y>85.5)=Pr(Y\ge86)\). Recall that to compute \(Pr(Y\ge86)\) the relationship \(Pr(Y\ge86)=1-Pr(Y\le85)\).
(answer3 <- round(pbinom(55,750,0.094) + (1 - pbinom(85,750,0.094)), 3))## [1] 0.06Compare 0.06 to the below:
(answer4 <- sum((props < 0.074 | props > 0.114 )) / 5000)## [1] 0.061The values from the simulated sampling distribution for \(p\) yields values close to the values from the exact sampling distribution.